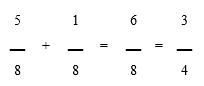Obiectivul învățării:
După finalizarea acestui modul, studentul ar trebui să știe semnificația procentului, cum să calculeze procente, cum să împartă întregul la numărul dorit de părți egale. Studenții ar trebui să știe care sunt fracțiile simple și când să le folosească.
Unul dintre cele mai comune moduri în care sunt folosite fracțiile este în domeniul banilor. Un sfert este 1/4 dintr-un euro, o zecime este 1/100 dintr-un euro. A cunoaște fracțiile și a ști cum să le comparați vă face să puteți gestiona banii mai ușor.
De asemenea, folosim fracțiile atunci când gătim. Ingredientele sunt, adesea, măsurate în fracții, de exemplu 1/4 kg în loc de 250 g.
Chiar și copiii mici se confruntă cu problema împărțirii unui măr în părți egale. Când își dau seama că niciunul dintre ei nu va primi tot mărul, împart mărul în două.
4.1 Fracții
Întregul (1) poate fi împărțit în părți mai mici, de exemplu în 2, 3, 4, 5 … și de câte ori avem nevoie. În plus, vom considera acele părți noi unități și chiar le vom putea număra:
O jumătate 1/2, două jumătăți 2/2, trei jumătăți 3/2; cinci jumătăți 5/2, etc.
Acestea sunt fracții simple.
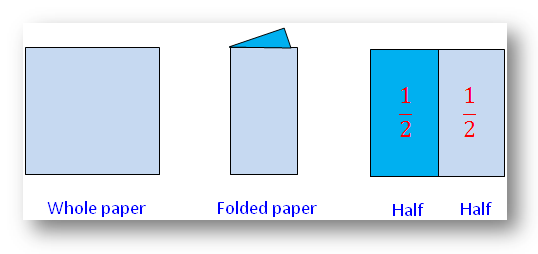
Fiecare parte egală dintr-un întreg care este împărțită în două, se numește o jumătate. Se exprimă ca 1/2 și se citește unu supra doi sau unu pe doi.
 Kilde
Kilde
Putem împărți în continuare foaia în patru părți egale. Fiecare parte egală se numește o pătrime sau un sfert din întreaga foaie. Astfel, orice întreg poate fi împărțit în patru părți egale și fiecare parte este un sfert sau o pătrime din întreg. Se exprimă ca 1/4 și se citește ca unul supra patru sau unu pe patru.
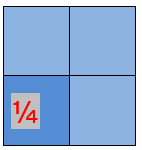
Fiecare parte a fracției are propria denumire:

Împărțiți o linie în 2, 3, 4 părți. Continuați să o împărțiți. Obținem tot mai multe linii. Dar intervalele lor sunt din ce în ce mai scurte. Iată câteva exemple de număr de segmente pe care le putem obține:

4.2 Suma fracțiilor