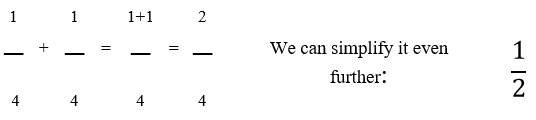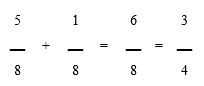Learning outcome: After completing this module the student should know the meaning of percent, how to calculate percentages, how to divide the whole into the desired number of equal parts. Students should know what fractions are called simple and when to use them.
One of the most common ways that fractions are used is money. A quarter is 1/4 of a euro, a dime is 1/100 of a euro. Knowing about fractions and how to compare them makes handling money much easier.
We also use fractions when we cook. Ingredients are often measured in fractions e.g. 1/4 kg instead of 250 g.
Even small children face the problem of sharing an apple equally. When they realize that none of them will get the whole apple, they split the apple in two parts.
4.1 Fractions
The one (1) can be divided to smaller parts, e.g. into 2, 3, 4, 5 … and as many times as we need. What‘s more, we will keep those parts as new units and even count them:
One half 1/2, two halves 2/2, three halves 3/2; five halves 5/2, etc.
These are simple fractions.
Each equal part of a whole that is divided in two is called one-half. It is expressed as 1/2 and read as one over two or one upon two.

Source
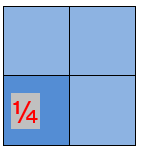
We can divide the sheet further into four equal parts. Each equal part is called one-fourth or a quarter of the whole sheet. Thus, any whole can be divided into four equal parts and each part is one-fourth or a quarter of the whole. It is expressed as 1/4 and read as one over four or one upon four.
Each part of the fraction has its own name:

Divide the same line into 2, 3, 4 parts. Continue to divide. We are getting more and more lines. Their intervals are getting shorter though. Here are some examples of the number of segments we can get:

4.2 Adding Fractions

Adding Fractions with same denominators
It is easy to add fractions with the same denominator (same bottom number):
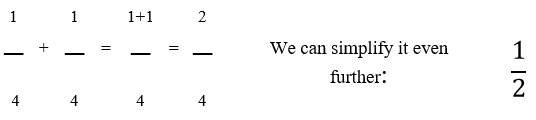
Again: 6/8 can be simplified to 3/4
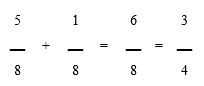
Adding Fractions with Different Denominators
What do we do when the denominators (the bottom numbers) are not the same?
3/8 + 1/4 = ?

We need to make them the same before we can continue, because we cannot add them like that. We must somehow make the denominators the same.
In this case it is easy, because we know that 1/4 is the same as 2/8 :
3/8 + 2/8 = 5/8

However, if the bottom numbers (denominators) are different to make them identical we should multiply the nominator and denominator of the smallest fraction (to keep it easy) by 2. We have to multiply both the top and bottom, by the same number to keep the value of the fraction unchanged.

4 is the smallest denominator, if we multiply by 2, we get 8. This leaves the value of the fraction the same. Now that the fractions have the same bottom number (“8”), we can continue adding.

Add the top numbers and put them over the same denominator, as shown below: